Cookies on this website

We use cookies to ensure that we give you the best experience on our website. If you click 'Accept all cookies' we'll assume that you are happy to receive all cookies and you won't see this message again. If you click 'Reject all non-essential cookies' only necessary cookies providing core functionality such as security, network management, and accessibility will be enabled. Click 'Find out more' for information on how to change your cookie settings.

Accept all cookies Reject all non-essential cookies

Logarithms and log-transformations

Data extraction tips for meta-analysis

Graphic image of two stick figure people with traffic light style heads

Logarithms (frequently referred to as ‘logs’) are often used in statistics. Medical statisticians log-transform skewed data to make the distribution of the data more symmetrical and this helps data ‘behave better’ by meeting the assumptions of statistical models. When plotting graphs, log-transforming makes curved data fall on lines which are more straight, and ‘flattens’ data, drawing in extreme values which enables patterns in the data to be seen more clearly.

In my blog, when I refer to logs I will mean ‘natural’ logs for which the base is e, known as Euler’s number, and it is equal to 2.718 to 3 decimal places. I will write the natural log of x as In(x). Medical statisticians typically use natural logs. In some sciences, logs to base 10, also known as the ‘common logarithm’ is more common. A bit of maths (see below if you’re interested) shows us

 log-correction-first-log.png

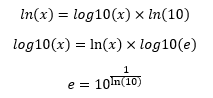
In computer programs and software packages, natural logs of x is written as log(x) in R and SAS, LN(x) in SPSS and EXCEL, and either ln(x) or log(x) in STATA. On calculators, the button to calculate the natural log of a number is ln. To antilog (cancel out) natural logs, we use the exponential function. This is written as exp(x) in R, SAS and STATA, and EXP(x) in SPSS and EXCEL. In calculators, it is given as ex, and this may have its own button, as on a mobile phone app, or it may be accessed on a hand-held calculator by pressing the SHIFT and ln keys in sequence.

Where did the equations come from?

To calculate ln(x):

Start with

𝑙𝑜𝑔10(𝑥)=𝑦

(equation 1)

Which means that

𝑥=10y

Taking natural logs of both sides

ln(𝑥)=ln(10y)

Using the 3rd law of logs 𝑙𝑛(𝑥𝑛)=𝑛×𝑙𝑛(𝑥)

ln(𝑥)=𝑦×ln(10)

Substitute for y using equation 1

ln(𝑥)=𝑙𝑜𝑔10(𝑥)×𝑙𝑛(10)

(equation 2)

To calculate log10(x):

By a similar process, starting with

𝑙𝑛(𝑥)=𝑦

(equation 3)

Which means that

𝑥=𝑒𝑦

Taking logs of base 10 of both sides and using 3rd law of logs

𝑙𝑜𝑔10(𝑥)=𝑦×𝑙𝑜𝑔10(𝑒)

Substitute for y using equation 3

𝑙𝑜𝑔10(𝑥)=ln(𝑥)×𝑙𝑜𝑔10(𝑒)

To calculate e:

Substitute for log10(x) in equation 2 and cancel out ln(x)

 1=𝑙𝑜𝑔10(𝑒)×𝑙𝑛(10)

Rearranging the equation

 log-table-1.png

Which means that

 Log-table-2.png

 

Download a pdf version of this tip

 

Dr Kathy Taylor teaches data extraction in Meta-analysis. This is a short course that is also available as part of our MSc in Evidence-Based Health Care, MSc in EBHC Medical Statistics, and MSc in EBHC Systematic Reviews.

Follow updates on this blog and related news on Twitter @dataextips